La matematica è ovunque intorno a noi! Quante volte abbiamo sentito questa frase, magari senza darle troppo peso? Eppure è una verità innegabile: dagli aspetti analitici a quelli geometrici, la matematica modella la nostra realtà quotidiana. Oggi voglio farti vedere il mondo con occhi nuovi, dando finalmente un nome a tutte quelle forme tridimensionali che incontriamo ogni giorno senza accorgercene.

Spero di aver catturato la tua attenzione, perché sto per trascinarti nel meraviglioso mondo delle quadriche! Niente paura, ci sarà un pizzico di matematica, ma nulla di troppo complicato. Se ti senti a tuo agio, segui pure il ragionamento; altrimenti, salta al prossimo paragrafo (fidati, è più semplice di quanto sembri). Fissiamo uno spazio proiettivo n-dimensionale: una quadrica è semplicemente l’insieme dei punti che soddisfa un’equazione di secondo grado in n+1 variabili. Facile, no? E se “spazio proiettivo” ti suona minaccioso, niente panico: è un ambiente matematico in cui anche le rette parallele si incontrano all’infinito.
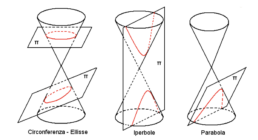
In parole povere, una quadrica non è altro che l’insieme delle soluzioni di un’equazione di secondo grado… con un sacco di incognite. Se fissiamo un sistema di riferimento e tracciamo questi punti, otteniamo delle forme geometriche ben precise, indovina quali?
Un po’ di storia
Quello che non ti ho ancora detto è che le quadriche, se le osserviamo in uno spazio proiettivo bidimensionale e ci limitiamo alla sua restrizione affine, non sono altro che le coniche che sicuramente hai incontrato al liceo.
Sì, proprio loro: circonferenze, ellissi, parabole… quelle che ti facevano venire il mal di pancia ogni volta che le incrociavi. Queste figure hanno una storia antichissima, che, come sempre quando si parla di matematica, affonda le radici nella Grecia classica.
Morris Kline, storico della matematica, non a caso scrisse: “Nella storia della civiltà i Greci occupano un posto preminente, nella storia della matematica sono l’evento supremo.”
Gli amici Greci
Il primo a parlare di coniche fu Menecmo, che le classificò studiando le intersezioni di piani con coni. Menecmo, in fondo, non ha fatto altro che tagliare un cono gelato (senza conoscere il gelato) ottenendo delle figure particolari, per poi assegnare loro dei nomi.
Il vero padre della teoria delle coniche fu, però, Apollonio, noto come “il grande geometra“. Fu lui a dare quei nomi che, con un po’ di fantasia, ricordano le caratteristiche di queste curve: iperbole=eccesso, parabola=somiglianza, ellisse=mancanza.
Tutto sto casino per parlarmi di cosa?
Ora che hai un’idea più chiara di cosa stiamo parlando, possiamo finalmente arrivare al punto. Se le coniche sono le quadriche nello spazio bidimensionale, è naturale aspettarsi che, passando alla terza dimensione, emergano figure familiari come sfere e cilindri. Ma… tutto qui? Un articolo intero solo per dirmi che esistono sfere e cilindri?
In realtà, esistono moltissime quadriche che incontri ogni giorno senza nemmeno saperlo. Sono ovunque, dalla natura all’architettura, dall’ingegneria al design. E allora, per farti scoprire il loro vero nome, ho raccolto alcuni esempi di strutture e oggetti che utilizzano queste forme geometriche. Preparati: una volta che li avrai visti, non potrai più ignorarli!

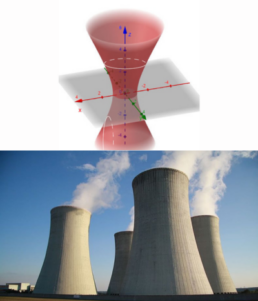
Iperboloide Iperbolico
Putin e Trump hanno a che fare ogni giorno con una particolare famiglia di quadriche: gli iperboloidi iperbolici (sì, lo so, sembra uno scioglilingua). Queste superfici hanno un ruolo fondamentale nella progettazione delle torri di raffreddamento degli impianti nucleari. Ma perché proprio questa forma?
Innanzitutto garantisce stabilità strutturale, ma il vero colpo di genio sta nella sua capacità di ottimizzare il raffreddamento: la superficie ampia facilita la dispersione del calore, mentre il restringimento centrale accelera il flusso del vapore grazie all’effetto Venturi.
Non chiedermi troppi dettagli: sono un matematico, mica un fisico! A seguire troverai un’immagine di una torre di raffreddamento e un modello di iperboloide su GeoGebra. Ti sfido a cercare altri iperboloidi nel mondo, piccolo indizio: pensa alla Sagrada Familia.
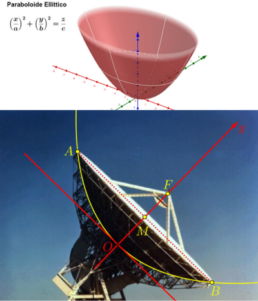
Paraboloide Ellittico
Ora ci spostiamo nella famiglia dei paraboloidi, in particolare quelli ellittici. La loro forma ricorda vagamente il mantello dell’invisibilità di Harry Potter. Nell’architettura non è facilissimo trovare esempi di paraboloidi ellittici, ma basta alzare un attimo lo sguardo sui tetti delle nostre case per scorgere qualcosa di molto familiare: le antenne paraboliche.
Forse la matematica non è così astratta come pensavi, eh? E se ancora non sei convinto, aspetta i prossimi due esempi: ti faranno saltare la testa!
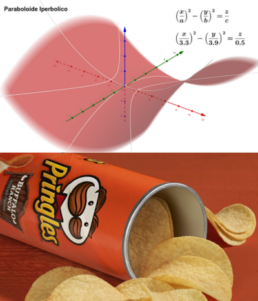
Paraboloide iperbolico
Non sei pronto per quello che sto per dirti… Il paraboloide iperbolico ha una forma così strana che a prima vista potrebbe sembrare difficile da trovare nel mondo reale. Ma basta cambiare prospettiva per accorgersi che assomiglia a due cose molto familiari: una sella da cavallo (da cui il nome paraboloide a sella) e, soprattutto, a qualcosa di decisamente più gustoso… le patatine Pringles!
La loro forma non è casuale, anzi: è stata studiata per ottimizzare lo spazio nella confezione e garantire la massima resistenza alle rotture. Un piccolo capolavoro di ingegneria… in un pacco di patatine. Semplicemente wow.
E la cosa ancora più assurda? Anche il loro tubo cilindrico è una quadrica. A questo punto mi viene il dubbio: le Pringles stanno cercando matematici da assumere?
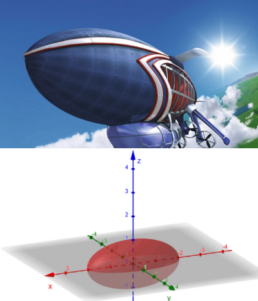
Ellissoide
Hai presente il cartone animato Lazy Town? Ora pensa al dirigibile del protagonista… dai, non dirmi che non hai mai sognato di salirci sopra!
Ti sei mai chiesto quale sia la sua forma geometrica? Io sì, e la risposta è: ellissoide. In fondo, ha perfettamente senso: un ellissoide non è altro che una rotazione di un’ellisse attorno a uno dei suoi assi. E non è certo l’unico esempio che puoi trovare nella vita reale.
Potrei elencartene a decine, come: L’Aspire Tower di Dubai, Il Planetarium di Saint Louis e perfino la Sydney Opera House, che può essere vista come un insieme di calotte sferiche incastrate tra loro. Insomma, la matematica è ovunque, anche nelle cose più inaspettate.
E ora che lo sai, scommetto che non guarderai più una patatina, un’antenna o un dirigibile con gli stessi occhi!
Fonti
Di seguito trovi le fonti dell’articolo:
Teoria proiettiva, affine e metrica delle quadriche di Eva Ferrara Dentice, qui il link per acquistare questo libro
Storia della matematica di Carl Boyer
Questo splendido video Youtube
Uso di Geogebra
2025-05-13
BAMBINI DA LABORATORIO
He Jankui, un biofisico cinese, ha sperimentato la modifica genetica sugli…
2025-04-30
Sophie Germain: la “Mulan” di Gauss
Il 30 aprile festeggiamo il compleanno di Gauss: quale occasione migliore per…
2025-04-16
Perché non riusciamo a sconfiggere l’HIV?
I virus non sono tutti uguali, ed alcuni di loro possono essere molto…
2025-04-02
Evo: giocare a scacchi con la genetica
L’IA evolve rapidamente: Evo 2 analizza il DNA, prevedendo mutazioni genetiche,…
2025-03-27
Tu sai studiare la Matematica?
Molti studenti imparano formule matematiche come fossero filastrocche. Testiamo…
2025-03-14
IL PI GRECO (NON) È UNA COSTANTE
II pi greco non vale sempre 3,14... Esistessero altre geometrie che influenzano…
2025-02-23
Er compleanno de Steve Jobs
In una classe di 23 persone la probabilità che due festeggino il compleanno lo…
2025-01-20
Chi taglia i capelli al barbiere?
Le domande esistenziali sono tante, ma la più importante è: "Chi taglia i…
2024-12-17
Equazioni di Maxwell: arte contemporanea
Cosa accomuna le equazioni di Maxwell e l'arte astratta? Entrambe sempre più…
2024-12-09
Un robot per amico: l’AI e le sue creature domestiche
L'AI riempie le mura domestiche nelle vesti di "coinquilina". Che tipo di…
2024-12-03
SMS: bei tempi… o forse no
Non facciamoci ingannare dalla nostalgia: gli SMS sono uno strumento…
2024-11-26
Safety Tutor: un motivo (in più) per odiare la matematica
Dietro le multe per eccesso di velocità si nasconde il teorema di Lagrange. Un…
2024-11-21
Smentire Omero con la fisica
Il fisico irlandese Samuel Haughton ha studiato il modo più efficace per…
2024-11-18
Gratta e Vinci: come diventare poveri
I Gratta e Vinci sono croce e delizia di molti italiani. Ma davvero ti…
Autore
-
Ciao, mi chiamo Massimo... da grande vorrei essere un matematico. Ora mi diverto semplicemente a tartassarti di notizie prendendo spunto dai miei studi. Nel tempo libero bevo succhi a pera!
Visualizza tutti gli articoli