Equazioni di Maxwell: arte contemporanea

Tra un pasto e l’altro del pranzo di Natale di due anni fa, zio Ugo, mosso da una ferocia intellettuale, mi prese il braccio e avvicinando la sua bocca al mio orecchio mi sussurrò: «Diffida da quei fisici che ti fanno una testa così sulle equazioni di Maxwell in forma covariante e poi non sanno risolvere un banale circuito o un piano inclinato!». Che massima. Ma che vuol dire?

Fine del liceo: ti porti dietro un’esperienza ormai quinquennale, sei una persona nuova (nel bene o nel male), si sta avvicinando l’esame, sei un po’ preoccupato ma sai che te la caverai, e poi c’è la gita di fine anno che promette tanto divertimento. Insomma, al diavolo tutti i momenti brutti e i pianti fatti, alla fine pensi «Si dai… mi mancherà tutto questo».

Poi arriva il prof di fisica e scrive questa roba sulla lavagna:

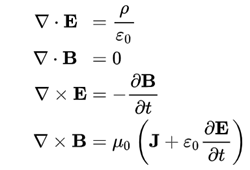
Ci ripensi. Eppure, per un fisico sono belle, bellissime, stupende; se campioniamo 100 fisici, almeno 90 le metteranno nella top 5 delle equazioni più belle. A te che sembra aramaico antico però voglio dire una cosa: il concetto, oltre a essere innegabilmente affascinante (non provare a dire di no) è in realtà semplice e veloce da capire.

L’oggetto delle equazioni è una delle love stories più belle della fisica: campo elettrico (E) e campo magnetico (B). Sono quattro, e fin qua ci siamo. Però si possono dividere in due gruppi. Le prime due equazioni ci danno alcune caratteristiche dei campi: il campo elettrico (E BASTA) fa certe cose, il campo magnetico (E BASTA) ne fa altre.

Le altre due sono di tipo relazionale: guarda, nella stessa equazione compare sia campo elettrico che campo magnetico. Il campo elettrico fa… cose e nasce il campo magnetico. Il campo magnetico fa altre cose e nasce il campo elettrico. Ma che cosa fanno ‘sti campi? Prendi una calamita, sappiamo che fa no? Genera un campo magnetico fatto così

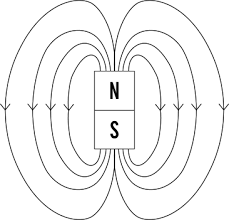
Prendi con la tua mano questa calamita e falla muovere attraverso una spira, un aggeggio che per semplicità immaginiamo circolare. Il flusso del campo magnetico, che è variabile perché lo stai muovendo, genera proprio una corrente elettrica nella spira: un bellissimo campo elettrico!

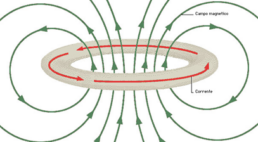
Possiamo così distinguere i due gruppi di equazioni in caso statico e caso dinamico: nel secondo i due campi si innamorano e si inseguono vicendevolmente. Beh dai, non è difficile no? Anzi, queste equazioni rappresentano qualcosa di concreto, in pieno spirito fisico. Questa prima versione è più come un cane che abbaia ma non morde. Passiamo alle altre.

Chiariamo subito: queste versioni differenti rappresentano comunque, alla fine della fiera, lo stesso concetto fisico. E allora perché esistono? Innanzitutto la prima di queste versioni è data da un’aggiunta nella notazione matematica che ha anche un rilievo fisico. Ha poi lo scopo di renderle visivamente più compatte: i due gruppi di due equazioni ciascuno diventano infatti due sole equazioni. Eccole:

Dove sono i nostri Romeo e Giulietta? Tutti addensati in quella F strana con gli apici greci, che no, non sono esponenti! Ti danno fastidio? Non sai leggere il greco? O peggio ancora, non sai se chiamarli «mu, nu» o «mi, ni»? Bene ecco a te la versione ancora più compatta e pulita

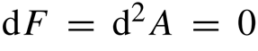
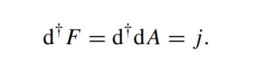
I fisici non le hanno scritte così però per te che non sai il greco antico, ma le hanno scritte così perché esistono concetti come fibrati e gruppi di gauge. Nomi strani e fidati… non vuoi sapere cosa sono.

Hai capito cosa sta succedendo? Dalla prima chill version siamo arrivati a quest’ultima versione, guadagnando in «pulizia dello stile» e perdendo inevitabilmente nella comprensione di quello che ci sta dietro. Il cambiamento più importante sta però in quella concretezza di prima, ora del tutto persa. Potrebbe forse venire così contaminato il rapporto, che la fisica ha sempre richiesto più che diretto e evidente, con la realtà?

Piet Mondrian, pittore olandese vissuto nel XX secolo (mentre la fisica viveva la più grande rivoluzione dopo quella galileiana), ha avuto un’evoluzione artistica assai interessante: un giorno dipinge un albero e lo fa così

Un altro giorno, o lo stesso albero o un altro, comunque sempre un albero, decide di farlo così

“Something happened” direbbero i nostri amici inglesi. E non avete visto cosa, un altro giorno ancora, Piet Mondrian arriva a fare

Ma cosa è successo? Da un punto di vista sempre e solo fenomenico (accontentiamoli gli amici filosofi e mettiamoci sti termini) è successo esattamente quello che abbiamo visto per le equazioni di Maxwell: lo stile sembra essersi pulito.

Penserai che realizzare l’ultimo di questi dipinti sia meno difficile perché più sintetico, eppure questo “risparmio visivo” (proprio come nelle notazioni delle equazioni) è avvenuto a discapito di una grossa perdita di comprensione. Più dettagli, più immediatezza (e viceversa). 

Insomma so’ sempre alberi, ma nell’ultimo dipinto lo capisci? So’ sempre campi elettromagnetici, ma nell’ultima equazione lo capisci? Dirai «vabbè, io non sono un fisico», ma fidati che hanno difficoltà a capire il senso in toto dell’ultima versione delle equazioni anche dei laureati alla triennale di fisica. 

Il percorso artistico di Mondrian si lega, si declina e prende forma in un contesto del tutto metafisico. Ma Mondrian è un artista, è interessato a parlare su un’altra lunghezza d’onda. I fisici, invece, devono ricordarsi e avere come monito quella chiarezza, semplicità e linearità per cui ha lottato gente come Galilei. Sono legati coi piedi per terra, così se per un attimo cominciano a immaginarsi le loro teorie nell’iperuranio vengono subito riportati giù.

Parla come mangi direbbe Zio Ugo. Ma attenzione! Le versioni finali che ti ho fatto vedere sono comunque importantissime, hanno dietro teorie matematiche anche molto eleganti, ma il fisico (perché di questa bestia si sta parlando) quando ci si approccia non deve MAI dimenticare la prima versione, il menu baby. È quello più diretto, quello che, in barba a fisici matematici e teorici, è il più fisico. Ogni tanto bisogna rivolgersi a Lui, Enrico Fermi, e rifare qualche esercizio di piano inclinato per tornare alla realtà.

Un po’ di sano elettromagnetismo lo trovi qui

Se vuoi invece distruggerti con tutta la matematica che ci sta dietro vai qui

Dipinti ancora più belli di Piet Mondrian