IL PI GRECO (NON) È UNA COSTANTE

Sì, bellissimi e tenerissimi i bimbi asiatici che alla recita dell’asilo ti recitano le prime 450 cifre del pi greco, ma lo sanno che il fantomatico rapporto circonferenza/diametro può essere anche più grande o più piccolo di quel 3,14159265…? Calma ingegneri! Non vi sto dando ragione, ma se siete comunque tra quelli che pensano che π=3 (o se siete bimbi asiatici) seguitemi. Andiamo a smontare la celebrità numero uno della matematica.

No, non potrai comunque vantarti con l’insegnante di matematica dicendo: <<Il pi greco non è una costante!>>, perché di fatto il pi greco è una costante. Bisogna solo capire in che senso costante: qualunque sia la circonferenza, il rapporto col suo diametro varrà sempre 3,14159… Quindi si potrebbe parlare di costante matematica? Sì, specificando quale matematica però. What? Sei saltato dalla sedia? Dai, me lo puoi dire che non ti aspettavi ci fossero più matematiche.

Di qualunque matematica si stia parlando, quello che adoro è che non deve dar conto di tutto il resto, quello che sta fuori (di essa), almeno quando si sta facendo ricerca teorica. Quindi sì, puoi dedurti equazioni che descrivono la rotazione della Terra P1ATta attorno al sole; nonostante la realtà empirica dica altro non ci sono problemi. Ai matematici puri interessa solo la coerenza interna della loro teoria. Capisci quindi ora che, decidendo in partenza cosa presupporre e cosa no (i postulati), nasca una moltitudine di combinazioni di teorie.

Definire la geometria è una sfida ardua, ti basti allora sapere che nucleo centrale di questa disciplina sono quattro postulati di un vecchio e gentile greco antico, Euclide, che però, se dobbiamo essere proprio sinceri, scrisse anche un quinto postulato, successivamente considerato il brutto anatroccolo. Per semplificare la questione, riporto qui un suo analogo

Data una qualsiasi retta e un punto esterno ad essa, esiste una e una sola retta che passa per quel punto e non interseca mai la retta data

Per fare matematica bisogna essere coraggiosi, e Girolamo Saccheri lo fu abbastanza nel negare questo postulato per in realtà dimostrarlo (dimostrare un postulato? Sì, questa roba dell’unicità della parallela non ha mai convinto nessuno per poterla presupporre e basta). Ma Saccheri poteva essere ancora più coraggioso; per fortuna lo furono altri per lui, i quali costruirono nuove geometrie sulla negazione di questo postulato.

• Più di una retta parallela 🡪 Geometria Iperbolica (costruita su una circonferenza, le rette sono le corde di questa circonferenza)
• Nessuna retta parallela 🡪 Geometria Ellittica (costruita sulla superficie di una sfera, le rette sono i cerchi massimi con centro il centro della sfera)

Una teoria matematica è affetta sempre da effetto domino: ritoccala da qualche parte e cambia (quasi) tutto. Bene, se ti dicessi che in queste geometrie, dopo aver modificato quel postulato, si è andati a modificare anche il valore di qualunque rapporto circonferenza/diametro e che non vale più 3,14159…? Proprio così.

Ho detto che i matematici puri non devono dar conto a nessuno delle loro teorie se non alle teorie stesse; vero, ma saremmo tutti più contenti se queste teorie si potessero applicare alla vita di tutti i giorni, e a quel punto sì che devono tener conto della realtà. Ora, non so quanto possa interessare alla vita di tutti i giorni sapere quale sia la geometria dello spazio, ma ad alcuni fisici e filosofi interessa davvero tanto (come a quei due simpaticoni di Newton e Kant). Gli studiosi del ‘600-‘700 non hanno fatto altro che adottare la geometria di nonno Euclide (quella dove il quinto postulato è vero, e dove quindi pi greco è una costante) e usarla per descrivere lo spazio costituente della realtà.

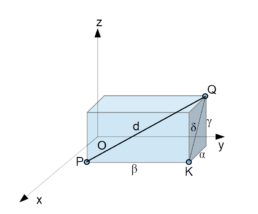
Ma che vuol dire geometria dello spazio? Facciamo un altro passo indietro: in fisica newtoniana (e non solo) dire cose come “Collino è fermo”, “Collino si muove a 3 m/s” non ha senso. Cioè, posizione e velocità sono relative e bisogna quindi sempre fissare un sistema di riferimento. L’accelerazione è però assoluta e Newton si chiede giustamente rispetto a cosa gli oggetti, quindi, accelerino. Postula l’esistenza di uno spazio assoluto, una sorta di palcoscenico dove succede semplicemente…tutto, e rispetto al quale fissare l’assolutezza di questa benedetta accelerazione. E di questo spazio che andiamo indagando la geometria, che Newton dice essere euclidea. Per inciso, anche il tempo è assoluto, ma staccato dallo spazio.

A inizio Novecento alcune scoperte scombinano le carte in tavola e si è così costretti a cambiare certi principi. Prontamente nel 1905 Einstein arriva e dice “Qui comando io!”: mette insieme spazio e tempo (anche questo è soggetto alla relatività accennata sopra) definendo lo spaziotempo assoluto. È sempre un palcoscenico universale, causa non causata di tutto il resto. Non ti suona come una cosa poco scientifica? Anche ad Einstein; cercava disperatamente una soluzione, e poi…

Si sa, Einstein amava la musica di Mozart, la ascoltava e la suonava. Leggenda narra che un giorno dell’anno 1915, vedendo su un vinile scendere delicatamente un ragnetto e lasciarsi trasportare dal girare come fosse in una giostra, si perse in una delle sue estasi scientifiche impersonificandosi nel ragnetto. Se fossi lì e con un piccolo campione di lunghezza misurassi prima la circonferenza del vinile e poi il diametro, otterrei il pi greco? Da fermo ovviamente sì, me lo ha detto prima nonno Euclide e poi Newton che ha euclidizzato tutta la realtà. Ma se il vinile cominciasse a girare, sarebbe la stessa cosa?

Il vinile che gira rispetto al vinile fermo (sistema inerziale) è un sistema non inerziale, cioè soggetto ad accelerazione costante. Ora seguimi per bene, c’è un passaggio delicatissimo che è, vuoi o non vuoi, la chiave di svolta. Se rispetto a un sistema di riferimento K osservo degli oggetti immobili, rispetto a un sistema di riferimento K’ che si allontana di accelerazione costante da K quegli stessi oggetti avranno tutti stessa accelerazione, anch’essa costante. Questione di prospettiva, Einstein però fa anche 2+2. Cioè? Il nostro Albert sapeva che un corpo immerso in un campo gravitazionale ha la stessa accelerazione costante indipendentemente dalla propria natura, e quindi quei corpi accelerati tutti rispetto a K’ non è come se fossero fermi ma immersi in un campo gravitazionale? Eureka!

Lo stesso vale per il vinile che gira, il sistema K’. Andando con un campione di lunghezza (un metro, un righello, Collino, qualunque cosa effettui misurazioni) a misurare la circonferenza, come Einstein aveva previsto per la sua precedente teoria del 1905, quello stesso campione subisce una contrazione dovuta al movimento rispetto al vinile fermo, la contrazione di Lorentz. Se l’oggetto con cui misuriamo si accorcia, la circonferenza misurata ne risulta più lunga. Facendo la stessa cosa per il diametro non succederà invece niente, perché questa contrazione funziona solo in direzione del moto (il diametro ha direzione perpendicolare alla direzione della rotazione). Quindi circonferenza maggiore/stesso diametro > π.

L’idea rivoluzionaria è però quella che leggi proprio qui sopra: per il principio di equivalenza esposto poco prima, quel sistema accelerato può essere considerato fermo ma immerso in un campo gravitazionale, il quale diventa responsabile della dis-euclidizzazione dello spaziotempo. Einstein risolve così anche il problema quasi filosofico dell’intangibilità di questo palcoscenico: il nuovo spaziotempo einsteiniano, a differenza di quello newtoniano, è partecipe della realtà fisica, si curva e si contorce, come fosse una strana spugna in cui siamo immersi. A dir la verità, ma qui apro le porte per altre migliaia di articoli, il campo gravitazionale è lo spaziotempo stesso.

Quindi potremmo dire che il π non è assolutamente una costante fisica, la realtà è tutt’altro che euclidea e la gravità se ne assume tutta la responsabilità. È sì una costante matematica, ma di quella piccola, piccolissima zona della matematica chiamata geometria euclidea.

• GEB, di D. Hofstadter
• Il Significato della Relatività, di A. Einstein
• Relatività Generale, di C. Rovelli